String matching is a fundamental problem in computer science, which involves finding the first occurrence of a given pattern in a text. This problem arises in many applications, such as searching for a character string in a text, finding a pattern in DNA sequences, decoding graphical or audio data, or searching for a sublist in linked lists. In this post, we will explore three different approaches to solving the string matching problem: a straightforward solution, the Rabin-Karp Algorithm, and the Boyer-Moore Algorithm. Also, this post is a lecture notes of the SC2001 course in NTU, covering common string matching algorithms.

Before we start, let’s define some notations:

$T$ is the text string
$P$ is the pattern string
$n$ is the length of $T$, $j$ is the position index of $T$
$m$ is the length of $P$, $k$ is the position index of $P$

SimpleScan Algorithm
Rabin-Karp Algorithm
- Rabin-Karp Algorithm with Hash Function
Boyer-Moore Algorithm
- Preprocessing - CharJump
- Preprocessing - MatchJump
Conclusion

SimpleScan Algorithm

int SimpleScan(char P[], char T[], int n, int m) {
    int i = 0;  // the current guess where P begins in T
    int j = 0;  // the index of the current character of T
    int k = 0;  // the index of the current character of P

    while (j < n) {
        if (T[j] != P[k]) {     // mismatch
            j = ++i;            // skip to the next guess
            if (i > n - m) {    // not have enough characters
                break;
            }
            k = 0;              // reset the index of P
        } else {                // match
            j++;
            k++;
            if (k == m) {       // found
                return i;
            }
        }
    }
    return -1;
}

Comparison starts with $k=0$ and $j=i$. When $k$ reaches $m$, all characters have been compared and matched.

When a mismatch happens, shift the pattern right one position: j=++i, k=0

The worst case happens when the pattern appears right at the end of the string, and each character in the text must be compared with each character in the pattern. This results in a time complexity of $O(mn)$, where $m$ and $n$ are the lengths of the pattern and the text respectively. For example, if the pattern is “aaaa” and the text is “aaaaaac”.

Furthermore, we can eliminate variable $i$ by using the fact $i = j - k$. This modification also mentioned in the tutorial.

Rabin-Karp Algorithm

To tell two strings are the same or not is much harder than telling two integers are the same or not. The main idea of Rabin-Karp Algorithm is to convert the given string slice into an integer.

The ourline of the Rabin-Karp Algorithm can be discribed as follows:

Convert the pattern (length $m$) to a number $p$
Convert the first $m$-characters (the first text window) to a number $t$
If $p$ and $t$ are equal, pattern found and exit
If not end-of-text, shift the text window one character right and convert the string in it to a number t, go to step $3$; else pattern not found and exit

To compute the number for the given string slice, we have the following notations:

$\Sigma$ is the set of all possible characters in the context. e.g. $\Sigma = {a, b, c, d}$
$d = |\Sigma|$ is the number of characters in $\Sigma$ or the size of the alphabet

The number $p$ of the pattern and the number t of the first $m$-character text window, are calculated iteratively. Take the example of the pattern $P$ “36451” and $d = 10$. The value of $p$ can be calculated as follows:

\[\begin{aligned} p &= 1 \times 10^0 + 5 \times 10^1 + 4 \times 10^2 + 6 \times 10^3 + 3 \times 10^4 \\ &= 1 + 50 + 400 + 6000 + 30000 = 36451 \end{aligned}\]

Or we can do it recursively:

int p = 0;
for (int i = 0; i < m; i++) {
    p = p * d + (P[i] - '0');
}

The calculation can be done in linear time.

To compute the number t after shifting the text window, it can be done in constant time based on the number of the previous text window. In general:

\[\text{new} = (\text{old} - \text{old's first character value} \times d^{m-1}) * d + \text{new's last character value}\]

$d^{m-1}$ here can be precomputed and stored, so the calculation can be done in constant time.

Rabin-Karp Algorithm with Hash Function

But when we have a long pattern and a long text, the calculation of $p$ will likely cause overflow. To avoid this, we hash the value by taking it mod a prime number $q$. And this prime number should be large. We can reorganize the steps as follows:

Hash the pattern to a number, $p_h$
Hash the first m-character text window to a number, $t_h$
If $p_h$ and $t_h$ are equal, compare the pattern with the text window. If equal, pattern found and exit
If not end-of-text, shift the text window one character right and (re)hash it to a number $t_h$, go to step 3; else pattern not found and exit

Note the fact that if $p_h = t_h$ not necessarily mean the pattern is found. But if $p_h \neq t_h$, the pattern is definitely not found.

To calculate value of a given string slice, we need to use a hash function $hash(txt, m, d)$:

int hash(int txt[], int m, int d) {
    int h = 0;
    for (int i = 0; i < m; i++) {
        h = h * d + txt[i];
        h %= q;
    }
    return h;
}

where $q$ is a large prime number, txt is the converted string slice (integer array), and $d$ is the size of the alphabet.

And to calculate the hash value of the next text window, we need to use a hash function $rehash(h, c, m, d)$:

int rehash(int h, int old_char, int new_char, int m, int d) {
    h = (h - old_char * d^(m-1)) * d + new_char;
    h %= q;
    return h;
}

where $h$ is the hash value of the previous text window, $old_char$ is the first character of the previous text window, $new_char$ is the last character of the new text window, and $d$ is the size of the alphabet. d^(m-1) can be precomputed and stored.

The whole Rabin-Karp Algorithm can be implemented as follows:

int RKscan(char P[], char T[], int n, int m) {
    int p = hash(P, m, d);
    int t = hash(T, m, d);
    for (int i = 0; i <= n - m; i++) {
        if (p == t) {
            if (strcmp(P, T + i) == 0) {
                return i;
            }
        }
        if (i < n - m) {
            t = rehash(t, T[i], T[i + m], m, d);
        }
    }
    return -1;    
}

The running time of Rabin-Karp algorithm in the worst case is $\theta((n - m + 1)m)$. However, in many applications, the expected running time is $O(n + m)$ plus the time required to process spurious hits. The algorithm requires $O(m)$ time for the two hash() calls and close to $O(n)$ time on the for loop. The number of spurious hits can be kept low by using a large prime number $q$ for the hash functions.

Boyer-Moore Algorithm

The Boyer-Moore Algorithm is a very efficient string searching algorithm. It processes the text being scanned, $T$, from left to right, and the pattern we are looking for, $P$, from right to left. To optimize the search, two tables are generated during preprocessing, which allow us to slide the pattern as far as possible after a mismatch. This algorithm is particularly efficient for long patterns.

int BMscan(char P[], char T[], int n, int m, int charJump[], int matchJump[]) {
    int k = m;  // the index of the current character of P, assume the string starts from index 1
    int j = m;  // the index of the current character of T, assume the string starts from index 1
    while (j <= n) {
        if (k <= 0)
            return j + 1; // match found
        if (P[k] == T[j]) {
            k--;
            j--;
        } else {            // mismatch
            j += max(charJump[T[j]], matchJump[k + 1]);
            k = m;
        }
    }
    return -1;
}

charJump and matchJump are the 2 tables generated in a preprocessing step.

Preprocessing - CharJump

The core idea of the charJump table is to compute the maximum number of characters to skip when a mismatch occurs by aligning the mismatched character with the rightmost occurrence of the same character in the pattern. Detailly:

If $T_j$ does not appear in $P$ at all, we line up $P$ after $T_j$
If $T_j$ occurs in $P$, we line up $T_j$ with the rightmost instance of $T_j$ in $P$

It is quite simple to compute the charJump table, the time complexity is $O(m + |\Sigma|)$.

void computeCharJump(char P[], int m, int charJump[]) {
    for (char ch = 0; ch < alpha; ch++)
        charJump[ch] = m;
    for (int i = 1; i <= m; i++)
        charJump[P[i]] = m - i;
}

where alpha is the size of the alphabet, and $m - i$ is the length from the current character position to the end of $P$. Notice that if a character appears more than once, we take the right-most occurrence.

Sometimes this heuristic fails, when charJump table gives a shorter jump than the length of the successful match $m - k$. In this case, we actually jump forward. Hence we need to choose the maximum of the two max(charJump[T[j]], m - k + 1). In this way, simplified BM (only charJump) algorithm can be implemented:

int BMscan(char P[], char T[], int n, int m, int charJump[], int matchJump[]) {
    int k = m;  // the index of the current character of P, assume the string starts from index 1
    int j = m;  // the index of the current character of T, assume the string starts from index 1
    while (j <= n) {
        if (k <= 0)
            return j + 1;   // match found
        if (P[k] == T[j]) {
            k--;
            j--;
        } else {            // mismatch
            j += max(charJump[T[j]], m - k + 1);
            k = m;
        }
    }
    return -1;
}

In some resources, the principal of charJump table is called bad character rule.

Preprocessing - MatchJump

This heuristic tries to derive the maximum shift from the structure of the pattern. It is defined for each of the characters (every position) in $P$. And we can roughly divide all possible situations into 3 cases:

Case 1: The matching suffix occurs earlier in the pattern, but preceded by a different character.

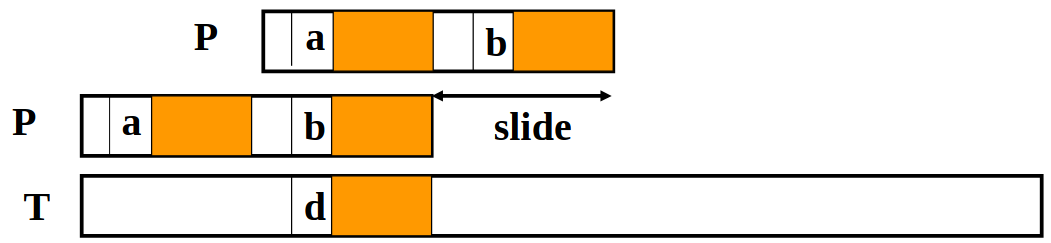
We line up the earlier occurrence of the suffix in $P$ with the matched substring in $T$.

Case 2: Only part of the matching suffix occurs at the beginning of the pattern (a prefix)

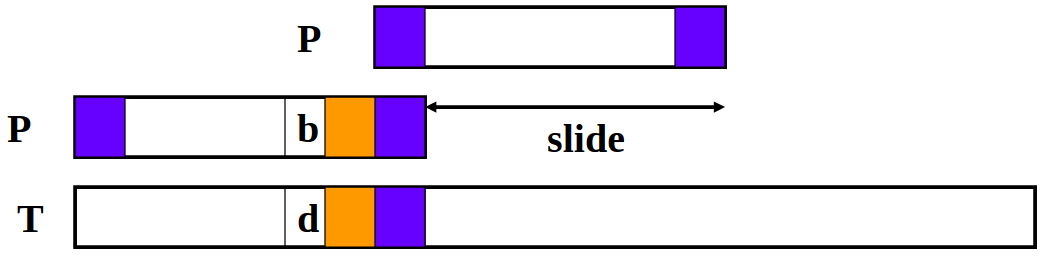
We line up the prefix in $P$ with part of the matched substring in $T$.

Case 3: There is no other occurrence of the matching suffix in the pattern. (Case 1 and Case 2 do not happen)

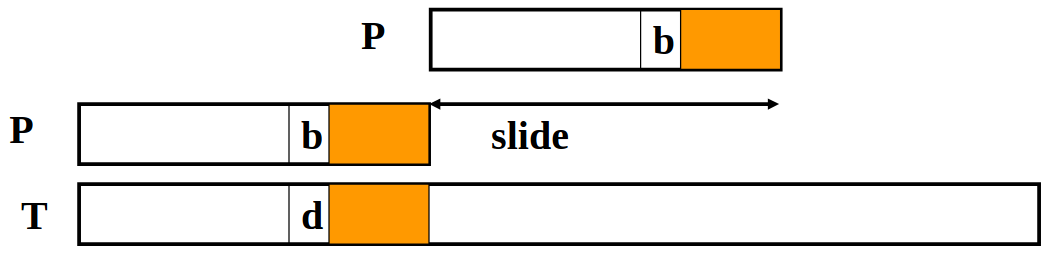
We line up $P$ after the matched substring in $T$.

In both cases, we can compute the matchJump value as follows:

\[\text{matchJump}(k) = \text{length of the repeated suffix in } P_{k, m} + \text{slide}(k)\]

where $P_{k, m}$ is the suffix of $P$ starting at position $k$ and length $m - k + 1$, and slide is the distance from the end (position $m$) to the end of the matched repeated suffix.

From the above analysis, before we compute matchJump, we need to compute two helpers array namely suffix and prefix. And definitions of the two helpers array are:

$\text{suffix}(k)$: The position of the first occurrence of the suffix of length $k$. $\text{suffix}(k) = j \implies P_{j, j + k - 1} = P_{m - k + 1, m}$
$\text{prefix}(k)$: Is the suffix of length k a prefix of the pattern string? $\text{prefix}(k) = \text{true} \implies P_{1, k} = P_{m - k + 1, m}$

To compute the helpers array, we can refer to the KMP algorithm. Or we can do it naively by scanning the pattern string from the end to the beginning:

void computeHelpers(char P[], int m, int suffix[], int prefix[]) {
    // initialize suffix and prefix
    for (int i = 1; i <= m; ++i) {
        suffix[i] = 0;
        prefix[i] = false;
    }

    for (int i = 1; i < m; ++i) {
        int j = i;  // the index of the first character to compare
        int k = 1;  // the length of the current matched suffix

        // match the suffix as far forward as possible
        while (j >= 1 && P[j] == P[m - k + 1]) {
            suffix[k] = j;
            j--;
            k++;
        }
        if (j == 1) {    // if the index goes at the bound, the current suffix is a prefix
            prefix[k] = true;
        }
    }
}

Then we can compute the matchJump table as follows:

void computeMatchJump(int m, int suffix[], int prefix[], int matchJump[]) {
    for (int k = 1; k < m; ++k) { 
        int j = m - k + 1;
        if (suffix[k]) { // case 1
            matchJump[j] = m - suffix[k] + 1;
        } else {
            // case 3
            matchJump[j] = m + k - 1;
            for (int i = j + 1; i <= m; ++i) {
                if (prefix[m - i + 1]) { // case 2
                    matchJump[j] = m + k - (m - i + 1);
                    break;
                }
            }
        }
    }
}

Also, the principal of matchJump table is called good suffix rule.

Conclusion

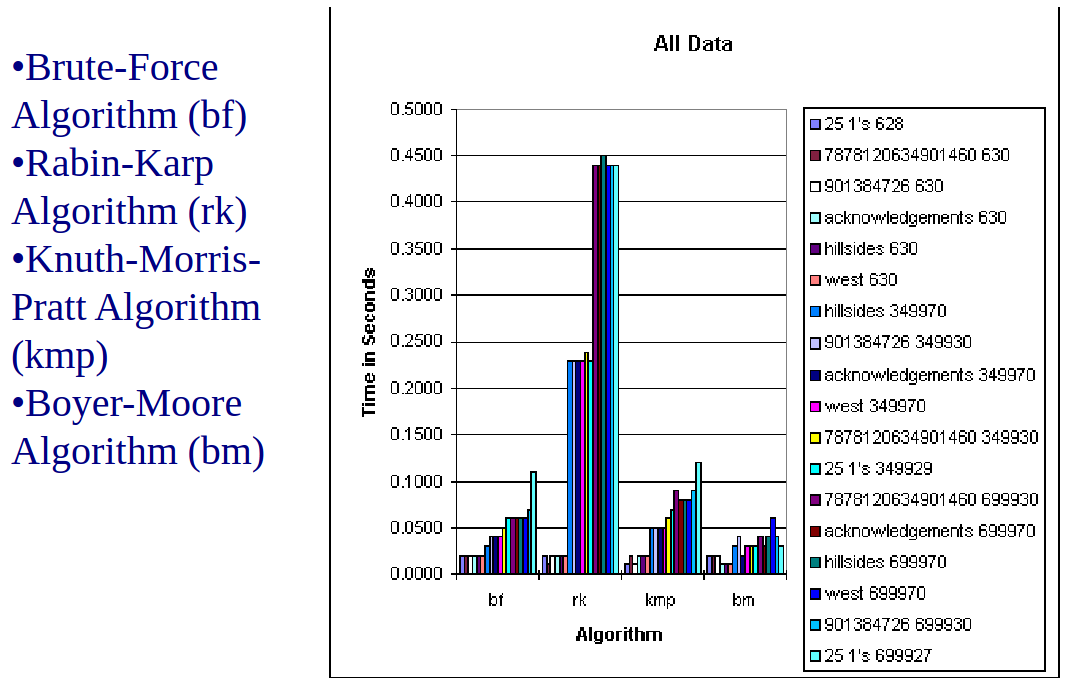
Brute Force performed better than expected because the worst-case scenario is rare, occurring when the pattern and text nearly match.
Rabin-Karp performed worse due to expensive function calls, costly division operations, and the time-consuming conversion of character values to numeric values.
The Boyer-Moore algorithm is generally the most efficient string-matching algorithm, particularly in text editors. Moore notes that the algorithm tends to perform faster with longer patterns.
For binary strings, the Knuth-Morris-Pratt algorithm is recommended.
For very short patterns, the brute force algorithm may be more effective.
Insights from the BM algorithm: Solving problems often requires a deep understanding of the problem’s structure. Analyze the problem thoroughly before devising a solution.

In my previous algorithm competition experience, I learned about the KMP algorithm and AC automaton on the topic of string matching. Maybe I will summarize the blogs about these two algorithms later.

String Matching

Table of Contents