Making Group Decisions: Voting

In the previous post, we examined how agents make decisions in two-agent games, focusing on the Nash Equilibrium. In this post, we will explore how a group of agents make decisions, delving into the realm of social choice theory. A classic example of social choice theory is voting, where the challenge is to combine individual preferences to derive a social outcome. This post discusses voting mechanism in group decision making in Lecture 10 of the SC4003 course in NTU. Let’s begin!
Table of Contents
- Notations and Definitions
- Voting Procedures: Plurality
- Sequential Majority Elections
- Voting Procedures: Borda Count
Notations and Definitions
Notation system make life easier when we are talking about something like voting. Let’s have a short definition of game theory notations, which will make the rest of this post easier to understand.
Components of a Social Choice Model
The set of voters (a.k.a agents in the context of the course) is defined as:
\[Ag = \{1, 2, \ldots, n\}\]Voters make group decisions with respect to a set of “outcomes” or “candidates”:
\[\Omega = \{\omega_1, \omega_2, ... \omega_3\}\]If $| \Omega | = 2$, say we have a pairwise election.
Preferences
Each voter has preferences over $\Omega$. It is an ordering over the set of possible outcomes $\Omega$. Take following wines as the example:
\[\Omega = \{ \text{gin}, \text{rum}, \text{brandy}, \text{whisky}\}\]The preference of agent $ray$ is denoted as:
\[\bar{\omega}_{ray} = \langle \text{whisky}, \text{rum}, \text{gin}, \text{brandy} \rangle\]which means that agent $ray$ prefers whisky to rum, rum to gin, gin to brandy, and brandy to whisky. These can also be written as:
\[\text{whisky} \succ_{ray} \text{rum} \succ_{ray} \text{gin} \succ_{ray} \text{brandy}\]The fundamental problem of social choice theory is to determine how to aggregate individual preference orders of voters into a collective decision that accurately represents the preferences of the group. This involves understanding how to merge diverse individual preferences into a coherent group preference. There are two primary approaches to preference aggregation: social welfare functions, which focus on ranking social states based on individual preferences, and social choice functions, which aim to select a single outcome from a set of alternatives.
Social Welfare Functions
The set of preference orderings over $\Omega$ is denoted as:
\[\pi(\Omega)\]A social welfare function $f$ takes the voter preferences order and produces a social preference order, e.g. beauty contest:
\[f: \pi(\Omega) \times \pi(\Omega) \times \ldots \times \pi(\Omega) \rightarrow \pi(\Omega)\]To denote the outcome comparison of a social welfare function:
\[\succ^*\]Sometimes, we want to select one of the possible candidates, rather than a social order. This gives social choice functions $f$, e.g. presidential election:
\[f: \pi(\Omega) \times \pi(\Omega) \times \ldots \times \pi(\Omega) \rightarrow \Omega\]Voting Procedures: Plurality
Social Choice Function, which selects a single outcome according to all preferences of the voters. Each candidate gets one point for every preference order that ranks them first. The winner is the one with the largest number of points. For example, Political elections in UK. If we have only two candidates, then plurality is a simple majority election.
Anomalies with Plurality
One anomaly with the plurality voting procedure is that it can produce a winner that is not supported by a majority of voters. For example, consider an election with $100$ voters and three candidates $\omega_1$, $\omega_2$, and $\omega_3$ where the distribution of votes is as follows:
- $40%$ of voters vote for $\omega_1$
- $30%$ of voters vote for $\omega_2$
- $30%$ of voters vote for $\omega_3$
In this scenario, ω1 would win the election with $40\%$ of the votes, even though a clear majority ($60\%$) of the voters prefer another candidate. This is a limitation of the plurality voting procedure in that it does not ensure that the winner is supported by a majority of the voters.
Strategic Manipulation by Tactical Voting
The concept of strategic manipulation by tactical voting is a phenomenon where a voter may vote for a candidate other than their true preference in order to achieve a better outcome. This can occur when a voter believes that their true preference is not viable, and that by voting for a second choice, they can prevent a less desirable candidate from winning. This is also known as strategic voting or insincere voting. For example, if a voter’s true preference is candidate $A$, but they believe that candidate $B$ is more likely to win than $A$, they may vote for $B$ in order to prevent candidate $C$ from winning, even if $B$ is not their true preference.
\[\text{Strategic voting: } \text{Vote for } B \text{ to prevent } C \text{ from winning}\]In this scenario, the voter is engaging in strategic manipulation of the vote, as they are not voting for their true preference. This can lead to a situation where the outcome of the election does not accurately reflect the true preferences of the voters. Let’s take a look at following example, suppose my preferences are:
\[\omega_1 \succ \omega_2 \succ \omega_3\]I believe $48.9\%$ of voters have preferences:
\[\omega_2 \succ \omega_1 \succ \omega_3\]and I believe $49.1\%$ of voters have preferences
\[\omega_3 \succ \omega_2 \succ \omega_1\]Then if I can represent $2\%$ of voters, I may do better voting for $\omega_2$ , even though this is not my true preference profile.
Condorcet’s Paradox
Condorcet’s paradox arises in voting scenarios where a majority preference cycle exists. Given a set of agents $Ag = {1, 2, 3}$ and outcomes $\Omega = {\omega_1, \omega_2, \omega_3}$, consider the preferences:
\[\begin{align*} \omega_1 & \succ_1 \omega_2 \succ_1 \omega_3 \\ \omega_3 & \succ_2 \omega_1 \succ_2 \omega_2 \\ \omega_2 & \succ_3 \omega_3 \succ_3 \omega_1 \end{align*}\]In this setup, for any candidate chosen, there exists another candidate preferred by a majority, leading to no clear winner. This exemplifies Condorcet’s paradox, where no option satisfies the majority.
Sequential Majority Elections
A variant of plurality, in which players play in a series of rounds: either a linear sequence or a tree (knockout tournament). We can use an example to understand this:
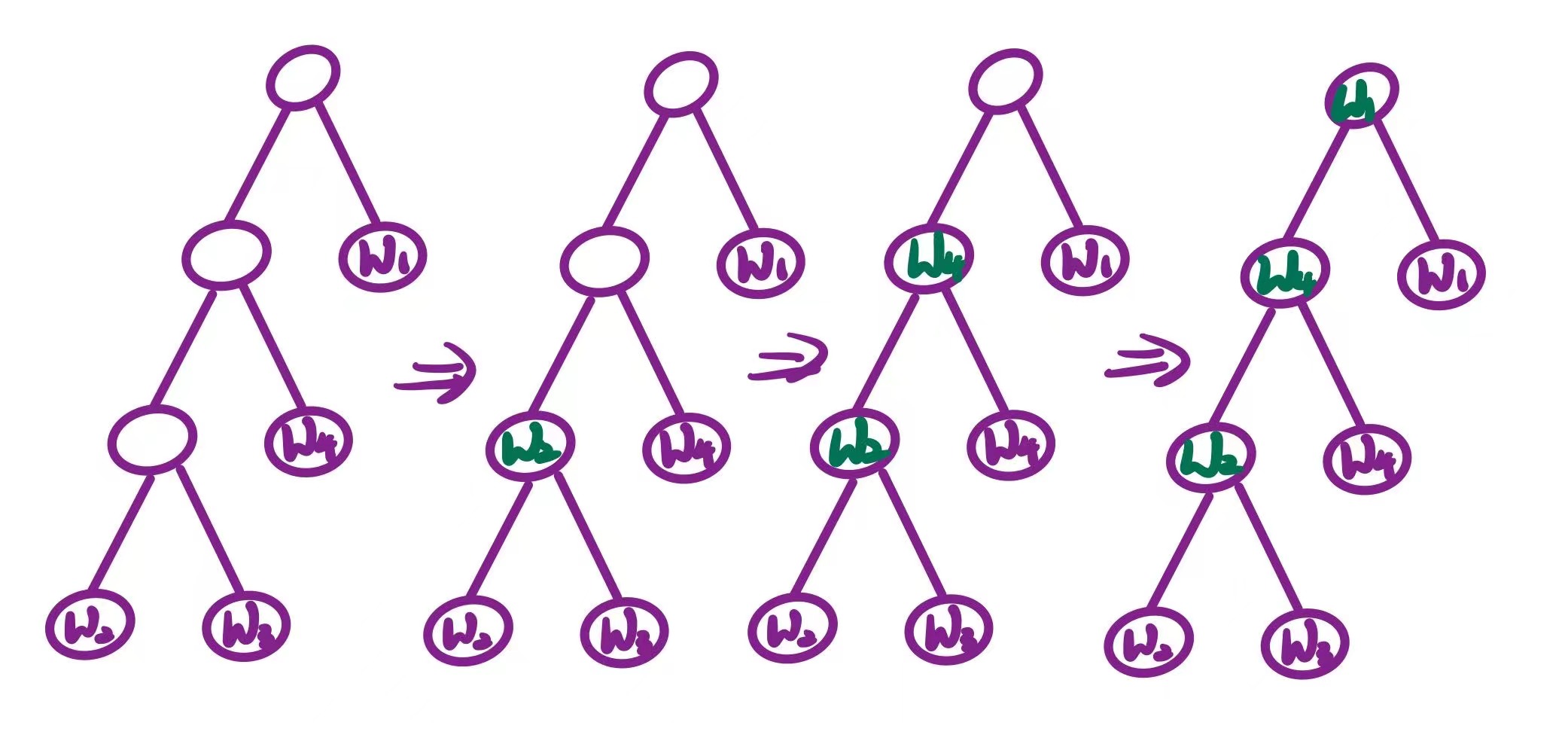
Anomalies with Sequential Pairwise Elections
Here, we pick an ordering of the outcomes,which determines who plays against who.For example, if the agenda is:
\[\langle \omega_2, \omega_3, \omega_4, \omega_1 \rangle\]Then the first election is between $\omega_2$ and $\omega_3$ , and the winner goes on to an election with \omega_4, and the winner of this election goes in an election with $\omega_1$. Anomalies can occur in sequential pairwise elections because the winner of an election may not be supported by a majority of the voters but depend on the agenda. Suppose we have:
\[\begin{align*} \text{33 voters prefer } & \omega_1 \succ \omega_2 \succ \omega_3 \\ \text{33 voters prefer } & \omega_3 \succ \omega_1 \succ \omega_2 \\ \text{33 voters prefer } & \omega_2 \succ \omega_3 \succ \omega_1 \end{align*}\]Then for every candidate, we can fix an agenda for that candidate to win in a sequential pairwise election! This can be demonstrated better using a majority graph.
Majority Graphs
This idea is easiest to illustrate by using a majority graph, which is a directed graph with:
- vertices represent candidates
- an edge $(i, j)$ if $i$ would beat $j$ is a simple majority election.
It is a compact representation of voter preferences. Let’s take a look at an example:
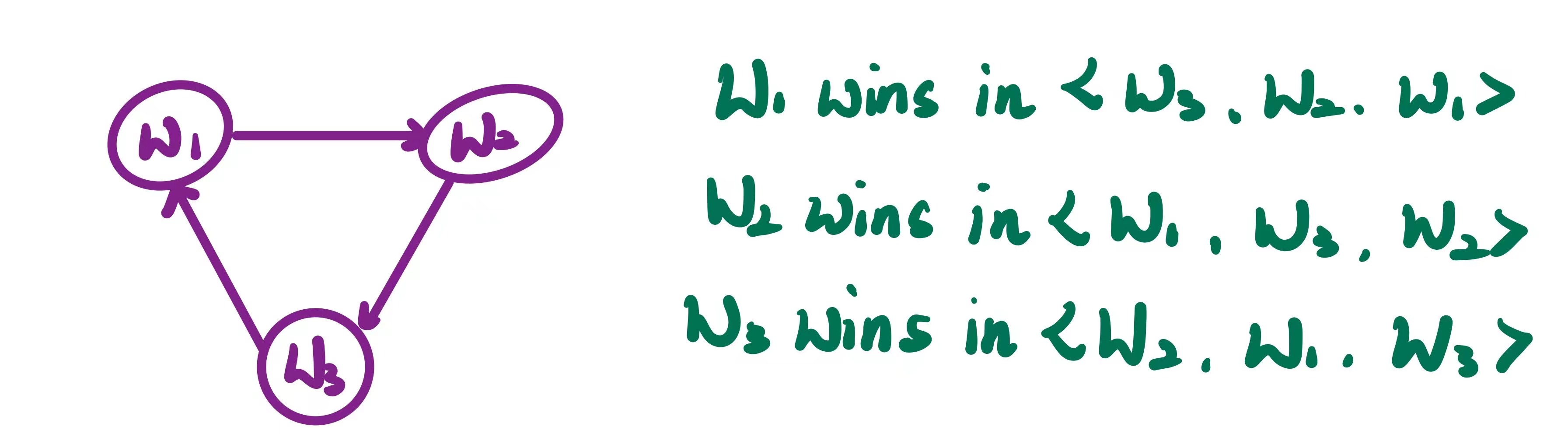
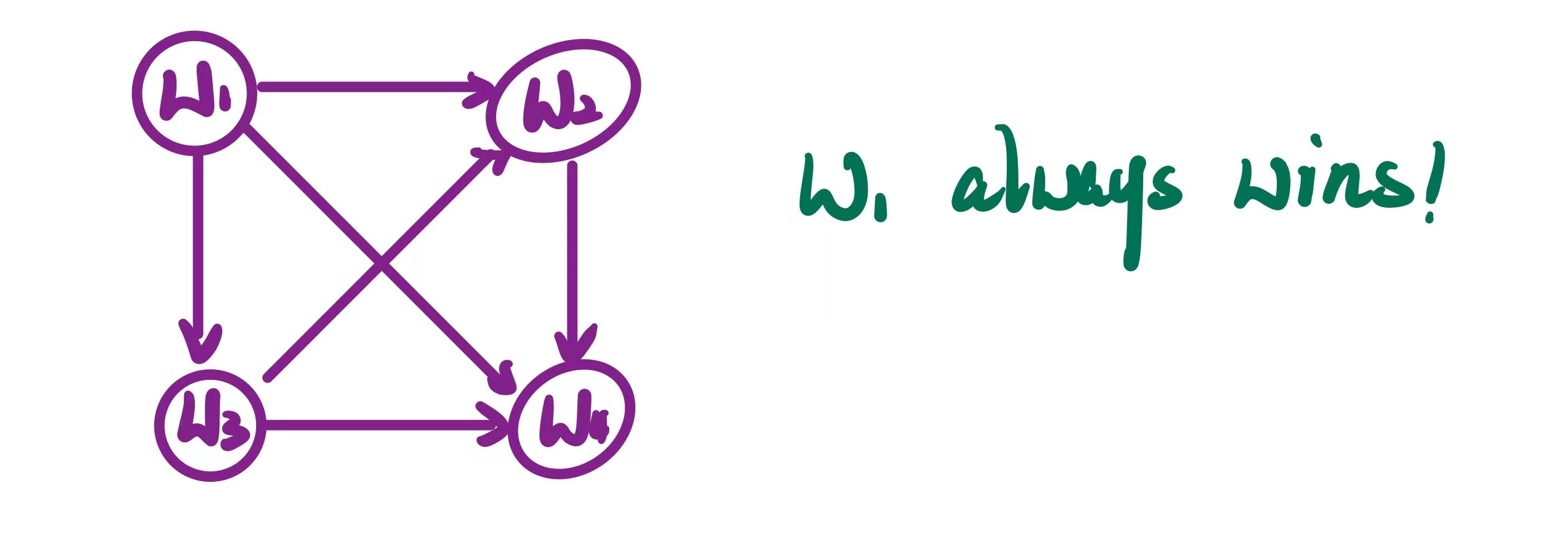
A Condorcet winner is a candidate that would beat every other candidate in a pairwise election. Like:
Voting Procedures: Borda Count
The Borda count is a voting procedure that takes into account the whole preference order of each voter, unlike the plurality voting procedure which only considers the top ranked candidate. In the Borda count, each candidate is assigned a score based on its position in each voter’s preference order. The score is calculated as follows: if a candidate appears first in a preference order, its score is incremented by $k-1$, where k is the number of candidates; if it appears second, its score is incremented by $k-2$, and so on, until the last candidate in the preference order has its score incremented by $0$. After all voters have been considered, the candidate with the highest score is declared the winner. This procedure is more representative of the voters’ true preferences than the plurality procedure, as it takes into account the strength of opinion in favour of each candidate.
Desirable Properties of Voting Procedures
A desirable voting procedure should satisfy two fundamental properties: the Pareto property and Independence of Irrelevant Alternatives (IIA).
-
The Pareto property states that if all voters prefer candidate $\omega_i$ over candidate $\omega_j$, then the social choice should also rank $\omega_i$ higher than $\omega_j$. This is a basic requirement that the social choice should respect the unanimous preference of the voters.
-
The IIA property states that the relative ranking of candidates $\omega_i$ and $\omega_j$ should only depend on the relative ranking of $\omega_i$ and $\omega_j$ in each voter’s preference order, and should not be affected by the introduction or removal of “irrelevant” alternatives. This property ensures that the social choice is focused on the true relative preferences of the voters, and is not influenced by external factors.
In summary, a desirable voting procedure should satisfy the Pareto property and the IIA property, which are two fundamental requirements for a fair and reasonable social choice.
Arrow’s Theorem
This theorem, proposed by economist Kenneth Arrow in 1951, reveals the fundamental impossibility of designing a fair and democratic voting system. The theorem states that:
In a situation with three or more candidates, any voting system that satisfies the Pareto property and the IIA property, must be a dictatorship, meaning that the final social ranking is determined by a single individual’s personal preference, without considering the opinions of others.
We initially hoped to design a fair and democratic voting system that respects the preferences of all individuals and is not influenced by irrelevant alternatives.
Arrow’s theorem proves that such a system is technically impossible, unless we allow a single individual to determine the outcome (i.e., a dictatorship).
The Gibbard-Satterthwaite Theorem
We already saw that sometimes, voters can benefit by strategically misrepresenting their preferences. Are there any voting methods which are non-manipulable, in the sense that voters can never benefit from misrepresenting preferences? The answer is given by the Gibbard-Satterthwaite Theorem:
In votes with three or more candidates, if a voting system is deterministic, non-authoritarian, and always produces a winner, then the system can be strategically manipulated.
which means no reasonable voting system can completely prevent voters from changing the outcome through dishonest voting. However, a news is that Computational Complexity can Help Rescue!
Bartholdi, Tovey, and Trick showed that there are elections that are prone to manipulation in principle, but where manipulation was computationally complex.”Single Transferable Vote” is a voting method that is NP-hard to manipulate!
Related Posts / Websites 👇
📑 Ray - NTU SC4003 Lecture 3 Note: Intelligent Agent Prolegomenon
📑 Ray - NTU SC4003 Lecture 4 Note: Agent Decision Making
📑 Ray - NTU SC4003 Lecture 5 Note: Agent Architecture
📑 Ray - NTU SC4003 Lecture 7 Note: Working Together Benevolent/Cooperative Agents
📑 Ray - NTU SC4003 Lecture 8 Note: Game Theory Foundations
📑 Ray - NTU SC4003 Lecture 9 Note: Allocating Scarce Resources: Auction
Comments